Everything You Need To Know About Work Energy Theorem

In this guide, we are going to do a complete analysis of the work energy theorem. At the end of it, you will understand how it works.

What is work in physics?

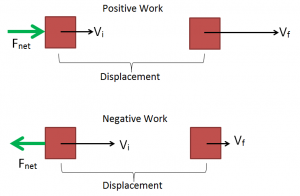
We can define work as a force acting on a body in the direction of another body. In this way, work is a vector. The force that does the work is called the ‘work-producing force’. It is also called the ‘force of production’, ‘the action of production’ or simply ‘the production force’.

The work-producing forces are:

1. Weight of the body on which it acts.
2. Friction forces acting between these bodies (if any). 3. Pressure forces acting between these bodies (if any).
3. Centripetal forces acting on a rotating body (if any).
4. Forces due to gravity acting on a rotating body (if any).
5. Electric potential energy stored in an electric field
6. Other forces in the frame of reference of the body making the work.
7. Forces due to external (non-centripetal) bodies acting on a body making work.
8. Forces due to other forces in the frame of reference of the body making work, etc.
9. Forces due to gravity acting on a rotating body.

What is energy?

We can define energy as the ability of a body to do work. In this way, energy is a scalar quantity. The amount of energy that a body has is called the ‘energy-potential’. It is also called the ‘potential energy, ‘the potential work’ or simply ‘the work potential’.

What does work energy theorem tell us?

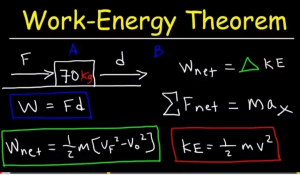
The theorem states that the work done by all the forces acting on a particle is equal to the particle’s kinetic energy.

Consider a force F applied to a mass m. The work done by this force is equal to the change in momentum of the system (m) due to this force (F). This change in momentum is equal to the rate at which momentum is being transferred from the system (m) to its surroundings (the ‘work energy’ must be conserved).

This means that if no external forces are acting on the system, then the work done by an applied force is always equal to the change in kinetic energy of the system.

Derivation

The derivation of the work energy theorem is based on a set of three simple assumptions:

The derivation proceeds by using these assumptions to calculate the work done by an applied force. This calculation shows that the work done by an applied force is always equal to the change in kinetic energy of the system.

Proof

The proof of the work energy theorem is based on the assumption that the system (m) is isolated from its surroundings. This assumption is justified because if there are external forces acting on the system, then these forces will change its momentum. Thus, for a system isolated from its surroundings, the product of force and change in momentum will be equal to zero.

This means that in general, the change in momentum of the system (Δp) is equal to the force acting on it (F).

The work done by an applied force is equal to the change in kinetic energy of the system. This means that, for a system isolated from its surroundings.

What is the work energy theorem equation?

This is the equation that shows that the work done by an applied force is equal to the change in kinetic energy of the system.

Consider a system subject to an external force (F) acting on it. The change in kinetic energy of this system, ΔK, may be calculated as:

Since F=F·m, we have:

We know that the change in momentum of a system is equal to the applied force times mass:

Since Δp=F·m, we have:

The work done by an applied force is equal to the change in kinetic energy of a system. This means that for a system isolated from its surroundings.

Work energy theorem potential energy

The work energy theorem can be applied to a system of particles connected by springs. The spring constant and force at each particle are known, and the total force acting on all particles is unknown. Using the work energy theorem, we can calculate the total force acting on all particles, which is equal to the sum of all other forces:

If everybody in a system gains or loses potential energy as a result of an applied force, then the total amount of work done by that force will be equal to the sum of the potential energies gained or lost by all bodies in that system.

In this case, we say that “the work performed by an applied force on a system of particles connected by springs is equal to the sum of their potential energies”. This is the basis of the kinetic theory of gases, in which the total amount of work done by gas molecules on each other is equal to their potential energy.

Work energy theorem with friction

In this theorem, we can also consider the friction force when calculating the work done by a force.

As we have mentioned earlier, work done=force * distance. When we consider friction, then it will be F=uN where N is the sliding force and u is the coefficient of friction.

So, the work done by friction force on a body is equal to the work performed by the given force on that body.

Work energy theorem with viscous forces

The work done by viscous forces is equal to the sum of the work performed by the force and the viscous force (which is equal to the change in potential energy).

This theorem is used in engineering to determine how much a body will deform when subjected to a given load. For example, if one applies a force of 100 N on an object, and finds that it deforms by 10 mm at its center, then we can calculate that the force must have been applied with an intensity of 80 N/m.

Work done by friction on an incline:

In this, other than friction, we have to consider another force: gravity. The work done by gravity is equal to the sum of all the forces acting on an object. While calculating the work done by friction, we must also consider gravity.

This will mean that work is done against both friction and gravity. To calculate the work done, we must know the distance covered by the body, the mass of the body, and the force acting on it.

We can also calculate work done against gravity if we know the mass of an object and its height above ground level.

Conclusion

In conclusion, I hope you have understood what work energy theorem is and the basic concepts of work energy theorem. If you have any questions or suggestions, please leave a message in the comments section below.

There is a lot to learn from the work energy theorem and there is a lot of misunderstanding about it. I hope this article will clear up some of those things and help you understand what work energy theorem is all about.

If you want to find more Electronic Components Distributors, please check out the following articles:

Electronic Components Distributors In the USA

Electronic Components Distributors In UK

Electronic Components Distributors In China

Electronic Components Distributors In India

Electronic Components Distributors In Singapore

Electronic Components Distributors In Malaysia

Electronic Components Distributors In Vietnam

Electronic Components Distributors In South Korea

Electronic Components Distributors In Taiwan

Electronic Components Distributors In Hong Kong